Reading Fractions

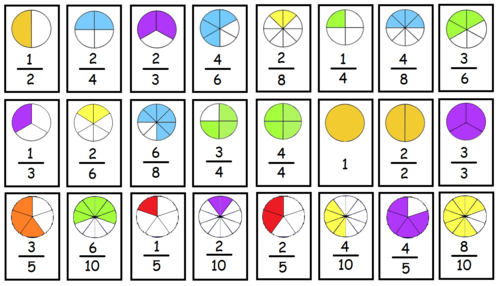
Slice a pizza, and we get fractions:

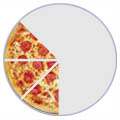1/2	1/4	3/8
(One-Half)	(One-Quarter)	(Three-Eighths)

The top number says how many slices we have. 
The bottom number says how many equal slices the whole pizza was cut into.

Some fractions may look different, but are really the same, for example: 

4/8	=	2/4	=	1/2
(Four-Eighths)		(Two-Quarters)		(One-Half)
	=		=

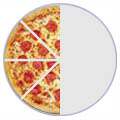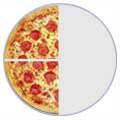It is usually best to show an answer using the simplest fraction ( ¹/₂ in this case ). That is calledSimplifying, or Reducing the Fraction

Numerator / Denominator

We call the top number the Numerator, it is the number of parts we have.
We call the bottom number the Denominator, it is the number of parts the whole is divided into.

NumeratorDenominator

You just have to remember those names! (If you forget just think "Down"-ominator)

Adding Fractions

It is easy to add fractions with the same denominator (same bottom number):

1/4	+	1/4	=	2/4	=	1/2
(One-Quarter)		(One-Quarter)		(Two-Quarters)		(One-Half)
	+		=		=

One-quarter plus one-quarter equals two-quarters, equals one-half

Another example:

5/8	+	1/8	=	6/8	=	3/4
	+		=		=

Five-eighths plus one-eighth equals six-eighths, equals three-quarters

Adding Fractions with Different Denominators

But what about when the denominators (the bottom numbers) are not the same? 

3/8	+	1/4	=	?
	+		=

Three-eighths plus one-quarter equals ... what?

We must somehow make the denominators the same.

In this case it is easy, because we know that ¹/₄ is the same as ²/₈ :

3/8	+	2/8	=	5/8
	+		=

Three-eighths plus two-eighths equals five-eighths

Arithmetic and Geometric Sequences

GAME

Addition add(ed) to all together both combined in all increase by more than perimeter plus sum total	Subtraction decreased by difference fewer than how many more left less less than minus remaining take away
Multiplication a area multiplied by of per product of rate times triple twice	Division divided  half how many each out of percent quarter quotient of percent

Solving math word problems

There are two steps to solving math word problems:

1. Translate the wording into a numeric equation
   that combines smaller "expressions"
2. Solve the equation!

Suggestions:

• Read the problem entirely
  Get a feel for the whole problem
• List information and the variables you identify
  Attach units of measure to the variables (gallons, miles, inches, etc.)
• Define what answer you need,
  as well as its units of measure
• Work in an organized manner
  Working clearly will help you think clearly
  • Draw and label all graphs and pictures clearly
  • Note or explain each step of your process;
    this will help you track variables and remember their meanings
• Look for the "key" words (above)
  Certain words indicate certain mathematical operations:

Math expressions (examples):
after you review the keywords, test yourself

addition: 5+x	subtraction: 5-x
multiplication: 5*x; 5x	division: 5 ÷ x; 5/x
Exercise: ("mouse over" the block for answer)
Key words for addition + increased by; more than; combined together; total of; sum; added to
What is the sum of 8 and y?	8 + y
Express the number (x) of apples increased by two	x + 2
Express the total weight of Alphie the dog (x) and Cyrus the cat (y)	x + y
Key words for Subtraction -  less than, fewer than, reduced by, decreased by, difference of
What is four less than y	y - 4
What is nine less than a number (y)	y - 9
What if the number (x) of pizzas was reduced by 6?	x - 6
What is the difference of my weight (x) and your weight (y)	x - y
Key words for multiplication * x or integers next to each other (5y, xy):of, times, multiplied by
What is y multiplied by 13	13y or 13 * y
Three runners averaged "y" minutes. Express their total running time:	3y
I drive my car at 55 miles per hour. How far will I go in "x" hours?	55x
Key words for division ÷ / per, a; out of; ratio of, quotient of; percent (divide by 100)
What is the quotient of y and 3	y/3 or y ÷ 3
Three students rent an apartment for $ "x" /month. What will each have to pay?	x/3 or x ÷ 3
"y" items cost a total of $25.00. Express their average cost:	25/y or 25 ÷ y

More vocabulary and key words:

• "Per" means "divided by"
  as "I drove 90 miles on three gallons of gas, so I got 30 miles per gallon."
  (Also 30 miles/gallon)
• "a" sometimes means "divided by"
  as in "When I filled up, I paid $10.50 for three gallons of gasoline,
  so the gas was 3.50 a gallon, or $3.50/gallon
• "less than"
  If you need to translate "1.5 less than x", the temptation is to write "1.5 - x". DON'T! Put a "real world" situation in, and you'll see how this is wrong: "He makes $1.50 an hour less than me." You do NOT figure his wage by subtracting your wage from $1.50.
  Instead, you subtract $1.50 from your wage
• "quotient/ratio of" constructions
  If a problems says "the ratio of x and y",
  it means "x divided by y" or x/y or x ÷ y
• "difference between/of" constructions
  If the problem says "the difference of x and y",
  it means "x - y"

What if the number (x) of children was reduced by six, and then they had to share twenty dollars? How much would each get?	20/(x - 6)
What is 9 more than y?	y + 9
What is the ratio of 9 more than y to y?	(y + 9)/y
What is nine less than the total of a number (y) and two	(y + 2) - 9 or  y - 7
The length of a football field is 30 yards more than its width "y". Express the length of the field in terms of its width y	y + 30

GAME

Johann Carl Friedrich Gauss

DECIMALS - 1ºESO

1. Candy is on sale 5 pounds for $9.95. Find the price per unit.

1. $10.00
2. $5.02
3. $1.99
4. $0.50

2. If candy is $4.25 per pound, how much would 3 pounds cost?

1. $12.75
2. $0.71
3. $1.28
4. $1.42

3. Ruby has $10. She buys a bottle of water for $1.29 and a bracelet for $5.95. How much change will she get back at the register?

1. $2.76
2. $7.24
3. $3.24
4. no change

4. At a clothing store, T-shirts are on sale for $9.97 each. What is the cost for 3 shirts?

1. $29.91
2. $27.91
3. $3.32
4. $12.9

5. Find the sum of 34.2 and 5.374.

1. 39.574
2. 28.826
3. 5.716
4. 185.7908

6. The student council bought 7 bags of apples for their fall party. Bags of apples were on sale for $3.45 each. How much did they pay for the apples?

1. $24.15
2. $0.49
3. $23.85
4. None of the above

7. One of the first helicopters flew at a speed of 44.7 km per hour. At this speed, ABOUT how far could the helicopter travel in 2.75 hours?

1. A little more than 135 km.
2. Exactly 135 km.
3. 47.45 km
4. A little less than 135 km.

8. A muffin recipe calls for 0.75 cups of blueberries. Paul is making 5 batches. He already has 2.5 cups of blueberries. How many more cups does he need?

1. 1 1/2 cups
2. 3.25 cups
3. 3.75 cups
4. 1.25 cups

Fibonacci Sequence

FIBONACCI PIANO - MUSIC

Agentes geológicos externos.

http://recursos-itaca.blogspot.com/2016/02/agentes-geologicos-externos.html

Los agentes geológicos externos (atmósfera, hielo, aguas superficiales, aguas subterráneas y seres vivos) modifican el relieve y el paisaje mediante procesos de meteorización, erosión, transporte y sedimentación.

El viento arrastra partículas en suspensión y modela el relieve. Los glaciares se desplazan lentamente por la superficie terrestre. Los ríos erosionan, transportan materiales y los depositan en sus desembocaduras. Las aguas subterráneas se almacenan formando acuíferos. Las aguas marinas ejercen mediante las olas, mares y corrientes una triple acción: erosión, transporte y sedimentación que dan lugar a estructuras características en las zonas costeras.

La Tierra se modela por la acción de los agentes geológicos externos. El agua, en sus diferentes formas, y el viento, transforman el paisaje.

El agua cuando cae en forma de precipitaciones arrastra materiales, ya sea cuando discurre en forma de aguas de arroyada, torrentes o formando ríos. Si se infiltra en el terreno forma acuíferos, si los materiales lo permiten.

Cuando las rocas son solubles, el agua las disuelve y forma estructuras espectaculares.

Si la temperatura es muy baja, el agua forma glaciares que avanzan lentamente por los valles.

El agua de los mares y océanos va esculpiendo las costas, proporcionándonos agradables playas e impresionantes acantilados.

El viento actúa sobre las regiones áridas del planeta, que no tienen una cubierta vegetal que les proteja de su acción. Las rocas adquieren formas fabulosas y aparecen mares de arena que avanzan poco a poco.

HLD 1º - Games

1. 1. GAMES
   2. 
      
   3. 
      
   4. Board Race
   5. Call My Bluff / Two Truths and A Lie
   6. Simon Says
   7. Word Jumble Race
   8. Hangman
   9. Pictionary
   10. The Mime
   11. Hot Seat
   12. Where Shall I Go?
   13. What’s My Problem?
   MUSIC FOR ESL