Como SIMPLIFICAR, SUMAR y RESTAR fracciones ALGEBRAICAS CANAL YOUTUBE

Welcome Georgia

Getting to know Georgia

JEOPARDY GAME

Central Angles and Inscribed Angles. Angle sum of any polygon

Geometry -1°eso

GAME

Repasar Ecuaciones en 1°ESO

https://www.edu.xunta.es/espazoAbalar/sites/espazoAbalar/files/datos/1291360755/contido/recurso/index.htm

Introducción al Álgebra

Algebra Basics: Solving Equations

GAME

Adding and Subtracting Fractions, Multiplying Fractions, and Dividing Fractions

GAME

MCM, MCD, reducción a común denominador y suma de fracciones

MCM

https://www.youtube.com/watch?v=-Vor5kKN4gI

MCD

https://www.youtube.com/watch?v=RGpZiQ17SH0

Suma de fracciones

https://www.youtube.com/watch?v=8C2sxLPLd48

Resolución de Problemas: Método de los 8 pasos

MÉTODO DE LOS OCHO PASOS PARA LA RESOLUCIÓN DE PROBLEMAS

DATOS

1. Leer y comprender el problema.
2. Realizar un dibujo esquemático del problema incluyendo los datos conocidos con sus unidades de medida.
3. Escribir los datos conocidos con sus valores y unidades de medida.
4. Escribir las incógnitas, con sus símbolos y unidades de medida.
5. Escribir las fórmulas o ecuaciones que se necesiten.

OPERACIÓN
6. Indicar los pasos a seguir (aplicación de leyes, cambios de unidades, cálculo de variables intermedias, despejar incógnitas, etc...), justificándolos y numerándolos.
7. Realizar las sustituciones necesarias y procedimientos con sus unidades de medida.

SOLUCIÓN
8. Resultado. Interpretación de los resultados obtenidos con sus unidades de medida.

COMPROBACIÓN
+ Dos pasos de control

9. Revisión de todos los pasos en busca de errores.
10. Análisis del resultado o resultados.

Information

1. Read and understand the problem.

2. Make a schematic drawing of the problem, including the known data with its units of measurement.

3. Write down the known data with its values and units of measurement.

4. Write down the unknown data with its symbols and units of measurement.

5. Note down any formulas or equations that are needed.

Operation

6. Indicate the number of steps to follow, i.e. application of laws, changes of units, calculation of intermediate variables, obvious unknown information etc., and justify them.

7. Carry out the necessary method and substitutions with their units of measure.

Solution

8. Result. Interpret the obtained results with their units of measurement.

Checking

+ Two control steps

 9. Review all the previous steps to find any errors.

10. Analyse the result(s).

FRACTIONS GAME

GAME

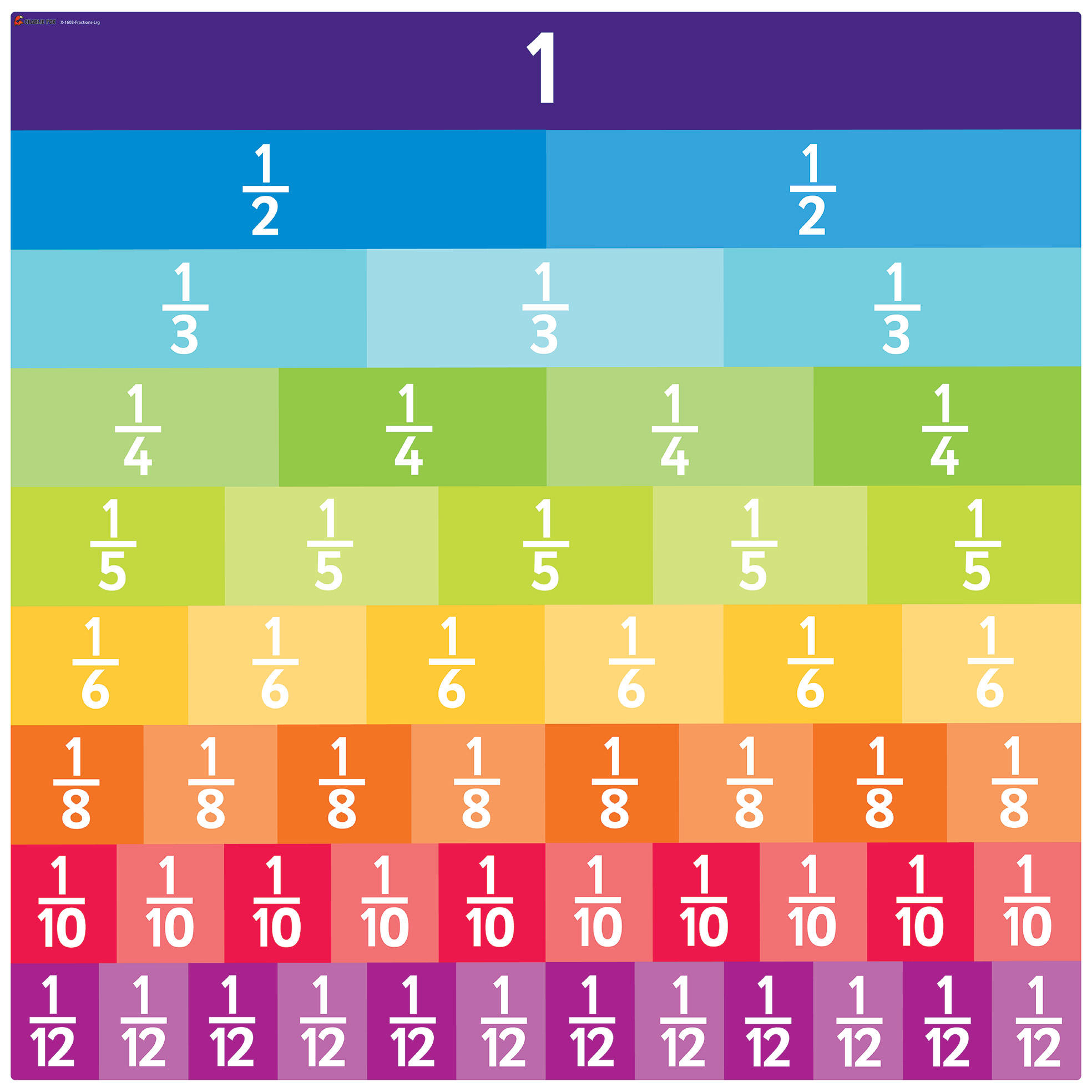
Reading Fractions

Slice a pizza, and we get fractions:

1/2	1/4	3/8
(One-Half)	(One-Quarter)	(Three-Eighths)

The top number says how many slices we have. 
The bottom number says how many equal slices the whole pizza was cut into.

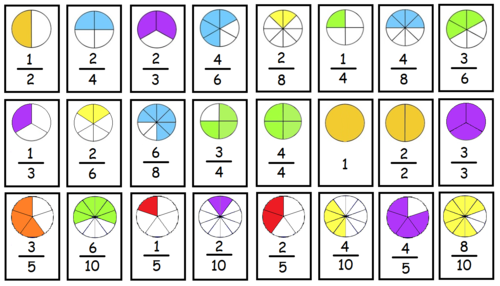
Some fractions may look different, but are really the same, for example: 

4/8	=	2/4	=	1/2
(Four-Eighths)		(Two-Quarters)		(One-Half)
	=		=

It is usually best to show an answer using the simplest fraction ( ¹/₂ in this case ). That is calledSimplifying, or Reducing the Fraction

Numerator / Denominator

We call the top number the Numerator, it is the number of parts we have.
We call the bottom number the Denominator, it is the number of parts the whole is divided into.

NumeratorDenominator

You just have to remember those names! (If you forget just think "Down"-ominator)

Adding Fractions

It is easy to add fractions with the same denominator (same bottom number):

1/4	+	1/4	=	2/4	=	1/2
(One-Quarter)		(One-Quarter)		(Two-Quarters)		(One-Half)
	+		=		=

One-quarter plus one-quarter equals two-quarters, equals one-half

Another example:

5/8	+	1/8	=	6/8	=	3/4
	+		=		=

Five-eighths plus one-eighth equals six-eighths, equals three-quarters

Adding Fractions with Different Denominators

But what about when the denominators (the bottom numbers) are not the same? 

3/8	+	1/4	=	?
	+		=

Three-eighths plus one-quarter equals ... what?

We must somehow make the denominators the same.

In this case it is easy, because we know that ¹/₄ is the same as ²/₈ :

3/8	+	2/8	=	5/8
	+		=

Three-eighths plus two-eighths equals five-eighths

Addition add(ed) to all together both combined in all increase by more than perimeter plus sum total	Subtraction decreased by difference fewer than how many more left less less than minus remaining take away
Multiplication a area multiplied by of per product of rate times triple twice	Division divided  half how many each out of percent quarter quotient of percent

Solving math word problems

There are two steps to solving math word problems:

1. Translate the wording into a numeric equation
   that combines smaller "expressions"
2. Solve the equation!

Suggestions:

• Read the problem entirely
  Get a feel for the whole problem
• List information and the variables you identify
  Attach units of measure to the variables (gallons, miles, inches, etc.)
• Define what answer you need,
  as well as its units of measure
• Work in an organized manner
  Working clearly will help you think clearly
  • Draw and label all graphs and pictures clearly
  • Note or explain each step of your process;
    this will help you track variables and remember their meanings
• Look for the "key" words (above)
  Certain words indicate certain mathematical operations:

Math expressions (examples):
after you review the keywords, test yourself

addition: 5+x	subtraction: 5-x
multiplication: 5*x; 5x	division: 5 ÷ x; 5/x
Exercise: ("mouse over" the block for answer)
Key words for addition + increased by; more than; combined together; total of; sum; added to
What is the sum of 8 and y?	8 + y
Express the number (x) of apples increased by two	x + 2
Express the total weight of Alphie the dog (x) and Cyrus the cat (y)	x + y
Key words for Subtraction -  less than, fewer than, reduced by, decreased by, difference of
What is four less than y	y - 4
What is nine less than a number (y)	y - 9
What if the number (x) of pizzas was reduced by 6?	x - 6
What is the difference of my weight (x) and your weight (y)	x - y
Key words for multiplication * x or integers next to each other (5y, xy):of, times, multiplied by
What is y multiplied by 13	13y or 13 * y
Three runners averaged "y" minutes. Express their total running time:	3y
I drive my car at 55 miles per hour. How far will I go in "x" hours?	55x
Key words for division ÷ / per, a; out of; ratio of, quotient of; percent (divide by 100)
What is the quotient of y and 3	y/3 or y ÷ 3
Three students rent an apartment for $ "x" /month. What will each have to pay?	x/3 or x ÷ 3
"y" items cost a total of $25.00. Express their average cost:	25/y or 25 ÷ y

More vocabulary and key words:

• "Per" means "divided by"
  as "I drove 90 miles on three gallons of gas, so I got 30 miles per gallon."
  (Also 30 miles/gallon)
• "a" sometimes means "divided by"
  as in "When I filled up, I paid $10.50 for three gallons of gasoline,
  so the gas was 3.50 a gallon, or $3.50/gallon
• "less than"
  If you need to translate "1.5 less than x", the temptation is to write "1.5 - x". DON'T! Put a "real world" situation in, and you'll see how this is wrong: "He makes $1.50 an hour less than me." You do NOT figure his wage by subtracting your wage from $1.50.
  Instead, you subtract $1.50 from your wage
• "quotient/ratio of" constructions
  If a problems says "the ratio of x and y",
  it means "x divided by y" or x/y or x ÷ y
• "difference between/of" constructions
  If the problem says "the difference of x and y",
  it means "x - y"

What if the number (x) of children was reduced by six, and then they had to share twenty dollars? How much would each get?	20/(x - 6)
What is 9 more than y?	y + 9
What is the ratio of 9 more than y to y?	(y + 9)/y
What is nine less than the total of a number (y) and two	(y + 2) - 9 or  y - 7
The length of a football field is 30 yards more than its width "y". Express the length of the field in terms of its width y	y + 30

GAME

DECIMALS - 1ºESO

1. Candy is on sale 5 pounds for $9.95. Find the price per unit.

1. $10.00
2. $5.02
3. $1.99
4. $0.50

2. If candy is $4.25 per pound, how much would 3 pounds cost?

1. $12.75
2. $0.71
3. $1.28
4. $1.42

3. Ruby has $10. She buys a bottle of water for $1.29 and a bracelet for $5.95. How much change will she get back at the register?

1. $2.76
2. $7.24
3. $3.24
4. no change

4. At a clothing store, T-shirts are on sale for $9.97 each. What is the cost for 3 shirts?

1. $29.91
2. $27.91
3. $3.32
4. $12.9

5. Find the sum of 34.2 and 5.374.

1. 39.574
2. 28.826
3. 5.716
4. 185.7908

6. The student council bought 7 bags of apples for their fall party. Bags of apples were on sale for $3.45 each. How much did they pay for the apples?

1. $24.15
2. $0.49
3. $23.85
4. None of the above

7. One of the first helicopters flew at a speed of 44.7 km per hour. At this speed, ABOUT how far could the helicopter travel in 2.75 hours?

1. A little more than 135 km.
2. Exactly 135 km.
3. 47.45 km
4. A little less than 135 km.

8. A muffin recipe calls for 0.75 cups of blueberries. Paul is making 5 batches. He already has 2.5 cups of blueberries. How many more cups does he need?

1. 1 1/2 cups
2. 3.25 cups
3. 3.75 cups
4. 1.25 cups

Primer día de clase

1. NORMAS DE CONDUCTA PARA LA CLASE DE MATEMÁTICAS

Sé respetuoso con la profesora y con los compañeros.

No te levantes de tu sitio asignado sin permiso.

Mantén un nivel de ruido adecuado y respeta la señal de ruido cero.

Levanta la mano si necesitas decir algo, los gritos y los aplausos están prohibidos.

Si copias en un examen, tu calificación será cero.

En las sesiones bilingües, intenta usar al máximo la lengua inglesa.

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

2. EVALUACIÓN DE LA MATERIA

1º ESO - Criterios de Evaluación

Números y Álgebra

1. Utilizar números naturales, enteros, fraccionarios, decimales y porcentajes sencillos, sus operaciones y propiedades para recoger, transformar e intercambiar información y resolver problemas relacionados con la vida diaria.

2. Conocer y utilizar propiedades y nuevos significados de los números en contextos de paridad, divisibilidad y operaciones elementales, mejorando así la comprensión del concepto y de los tipos de números.

3. Desarrollar, en casos sencillos, la competencia en el uso de operaciones combinadas como síntesis de la secuencia de operaciones aritméticas, aplicando correctamente la jerarquía de las operaciones o estrategias de cálculo mental.

4. Elegir la forma de cálculo apropiada (mental, escrita o con calculadora), usando diferentes estrategias que permitan simplificar las operaciones con números enteros, fracciones, decimales y porcentajes y estimando la coherencia y precisión de los resultados obtenidos.

5. Utilizar diferentes estrategias (empleo de tablas, obtención y uso de la constante de proporcionalidad, reducción a la unidad, etc.) para obtener elementos desconocidos en un problema a partir de otros conocidos en situaciones de la vida real en las que existan variaciones porcentuales y magnitudes directa o inversamente proporcionales.

6. Analizar procesos numéricos cambiantes, identificando los patrones y leyes generales que los rigen, utilizando el lenguaje algebraico para expresarlos, comunicarlos, y realizar predicciones sobre su comportamiento al modificar las variables, y operar con expresiones algebraicas.

7. Utilizar el lenguaje algebraico para simbolizar y resolver problemas mediante el planteamiento de ecuaciones de primer, segundo grado y sistemas de ecuaciones, aplicando para su resolución métodos algebraicos o gráficos y contrastando los resultados obtenidos.

Geometría

1. Reconocer y describir figuras planas, sus elementos y propiedades características para clasificarlas, identificar situaciones, describir el contexto físico, y abordar problemas de la vida cotidiana.

2. Utilizar estrategias, herramientas tecnológicas y técnicas simples de la geometría analítica plana para la resolución de problemas de perímetros, áreas y ángulos de figuras planas, utilizando el lenguaje matemático adecuado expresar el procedimiento seguido en la resolución.

3. Reconocer el significado aritmético del Teorema de Pitágoras (cuadrados de números, ternas pitagóricas) y el significado geométrico (áreas de cuadrados construidos sobre los lados) y emplearlo para resolver problemas geométricos.

4. Analizar e identificar figuras semejantes, calculando la escala o razón de semejanza y la razón entre longitudes, áreas y volúmenes de cuerpos semejantes.

5. Analizar distintos cuerpos geométricos (cubos, ortoedros, prismas, pirámides, cilindros, conos y esferas) e identificar sus elementos característicos (vértices, aristas, caras, desarrollos planos, secciones al cortar con planos, cuerpos obtenidos mediante secciones, simetrías, etc.).

6. Resolver problemas que conlleven el cálculo de longitudes, superficies y volúmenes del mundo físico, utilizando propiedades, regularidades y relaciones de los poliedros.

Funciones

1. Conocer, manejar e interpretar el sistema de coordenadas cartesianas.

2. Manejar las distintas formas de presentar una función: lenguaje habitual, tabla numérica, gráfica y ecuación, pasando de unas formas a otras y eligiendo la mejor de ellas en función del contexto.

3. Comprender el concepto de función. Reconocer, interpretar y analizar las gráficas funcionales.

4. Reconocer, representar y analizar las funciones lineales, utilizándolas para resolver problemas.

Estadística y probabilidad

1. Formular preguntas adecuadas para conocer las características de interés de una población y recoger, organizar y presentar datos relevantes para responderlas, utilizando los métodos estadísticos apropiados y las herramientas adecuadas, organizando los datos en tablas y construyendo gráficas, calculando los parámetros relevantes y obteniendo conclusiones razonables a partir de los resultados obtenidos.

2. Utilizar herramientas tecnológicas para organizar datos, generar gráficas estadísticas, calcular parámetros relevantes y comunicar los resultados obtenidos que respondan a las preguntas formuladas previamente sobre la situación estudiada.

3. Diferenciar los fenómenos deterministas de los aleatorios, valorando la posibilidad que ofrecen las matemáticas para analizar y hacer predicciones razonables acerca del comportamiento de los aleatorios a partir de las regularidades obtenidas al repetir un número significativo de veces la experiencia aleatoria, o el cálculo de su probabilidad.

4. Inducir la noción de probabilidad a partir del concepto de frecuencia relativa y como medida de incertidumbre asociada a los fenómenos aleatorios, sea o no posible la experimentación.

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

3º ESO MAC- Criterios de Evaluación

NÚMEROS Y ÁLGEBRA

1. Utilizar las propiedades de los números racionales para operarlos, utilizando la forma de cálculo y notación adecuada, para resolver problemas de la vida cotidiana, y presentando los resultados con la precisión requerida.

2. Obtener y manipular expresiones simbólicas que describan sucesiones numéricas, observando regularidades en casos sencillos que incluyan patrones recursivos.

3. Utilizar el lenguaje algebraico para expresar una propiedad o relación dada mediante un enunciado, extrayendo la información relevante y transformándola.

4. Resolver problemas de la vida cotidiana en los que se precise el planteamiento y resolución de ecuaciones de primer y segundo grado, ecuaciones sencillas de grado mayor que dos y sistemas de dos ecuaciones lineales con dos incógnitas, aplicando técnicas de manipulación algebraicas, gráficas o recursos tecnológicos, valorando y contrastando los resultados obtenidos.

GEOMETRÍA

1. Reconocer y describir los elementos y propiedades características de las figuras planas, los cuerpos geométricos elementales y sus configuraciones geométricas.

2. Utilizar el teorema de Tales y las fórmulas usuales para realizar medidas indirectas de elementos inaccesibles y para obtener las medidas de longitudes, áreas y volúmenes de los cuerpos elementales, de ejemplos tomados de la vida real, representaciones artísticas como pintura o arquitectura, o de la resolución de problemas geométricos.

3. Calcular (ampliación o reducción) las dimensiones reales de figuras dadas en mapas o planos, conociendo la escala. 4. Reconocer las transformaciones que llevan de una figura a otra mediante movimiento en el plano, aplicar dichos movimientos y analizar diseños cotidianos, obras de arte y configuraciones presentes en la naturaleza.

5. Identificar centros, ejes y planos de simetría de figuras planas y poliedros.

6. Interpretar el sentido de las coordenadas geográficas y su aplicación en la localización de puntos.

FUNCIONES

1. Conocer los elementos que intervienen en el estudio de las funciones y su representación gráfica.

2. Identificar relaciones de la vida cotidiana y de otras materias que pueden modelizarse mediante una función lineal valorando la utilidad de la descripción de este modelo y de sus parámetros para describir el fenómeno analizado.

3. Reconocer situaciones de relación funcional que necesitan ser descritas mediante funciones cuadráticas, calculando sus parámetros y características.

ESTADÍSTICA Y PROBABILIDAD

1. Elaborar informaciones estadísticas para describir un conjunto de datos mediante tablas y gráficas adecuadas a la situación analizada, justificando si las conclusiones son representativas para la población estudiada.

2. Calcular e interpretar los parámetros de posición y de dispersión de una variable estadística para resumir los datos y comparar distribuciones estadísticas.

3. Analizar e interpretar la información estadística que aparece en los medios de comunicación, valorando su representatividad y fiabilidad.

4. Estimar la posibilidad de que ocurra un suceso asociado a un experimento aleatorio sencillo, calculando su probabilidad a partir de su frecuencia relativa, la regla de Laplace o los diagramas de árbol, identificando los elementos asociados al experimento.

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

2ºFPB CIENCIAS APLICADAS - Resultados de aprendizaje y criterios de evaluación.

1. Trabaja en equipo profundizando en las estrategias propias del trabajo cooperativo.

a) Se ha debatido sobre los problemas del trabajo en equipo.

b) Se han elaborado unas normas para el trabajo por parte de cada equipo.

c) Se ha trabajado correctamente en equipos formados atendiendo a criterios de heterogeneidad.

d) Se han asumido con responsabilidad distintos roles para el buen funcionamiento del equipo.

e) Se ha usado el cuaderno de equipo para realizar el seguimiento del trabajo.

f) Se han aplicado estrategias para solucionar los conflictos surgidos en el trabajo cooperativo.

g) Se han realizado trabajos de investigación de forma cooperativa usando estrategias complejas.

2. Usa las TIC responsablemente para intercambiar información con sus compañeros y compañeras, como fuente de conocimiento y para la elaboración y presentación del mismo.

a) Se han usado correctamente las herramientas de comunicación social para el trabajo cooperativo con los compañeros y compañeras.

b) Se han discriminado fuentes fiables de las que no lo son.

c) Se ha seleccionado la información relevante con sentido crítico.

d) Se ha usado Internet con autonomía y responsabilidad en la elaboración de trabajos e investigaciones.

e) Se ha profundizado en el conocimiento de programas de presentación de información (presentaciones, líneas del tiempo, infografías, etc)

3. Estudia y resuelve problemas relacionados con situaciones cotidianas o del perfil profesional, utilizando elementos básicos del lenguaje matemático y sus operaciones y/o herramientas TIC, extrayendo conclusiones y tomando decisiones en función de los resultados.

a) Se han operado números naturales, enteros y decimales, así como fracciones, en la resolución de problemas reales, bien mediante cálculo mental, algoritmos de lápiz y papel o con calculadora, realizando aproximaciones en función del contexto y respetando la jerarquía de las operaciones.

b) Se ha organizado información y/o datos relativos al entorno profesional en una hoja de cálculo usando las funciones más básicas de la misma: realización de gráficos, aplicación de fórmulas básicas, filtro de datos, importación y exportación de datos.

c) Se han usado los porcentajes para analizar diferentes situaciones y problemas relacionadas con las energías.

d) Se han concretado propiedades o relaciones de situaciones sencillas mediante expresiones algebraicas.

e) Se han simplificado expresiones algebraicas sencillas utilizando métodos de desarrollo y factorización.

f) Se ha conseguido resolver problemas reales de la vida cotidiana en los que se precise el planteamiento y resolución de ecuaciones de primer grado y sistemas de ecuaciones.

g) Se han resuelto problemas sencillos que requieran el uso de ecuaciones utilizando el método gráficos y las TIC.

h) Se ha utilizado el vocabulario adecuado para la descripción de situaciones relacionadas con el azar.

i) Se han aplicado las propiedades de los sucesos y la probabilidad.

j) Se han resueltos problemas cotidianos mediante cálculos de probabilidad sencillos.

4. Resuelve problemas sencillos de diversa índole, a través de su análisis contrastado y aplicando las fases del método científico.

a) Se han planteado hipótesis sencillas, a partir de observaciones directas o indirectas recopiladas por

distintos medios.

b) Se han analizado las diversas hipótesis y se ha emitido una primera aproximación a su explicación.

c) Se han planificado métodos y procedimientos experimentales sencillos de diversa índole para refutar o

no su hipótesis.

d) Se ha trabajado en equipo en el planteamiento de la solución.

e) Se han recopilado los resultados de los ensayos de verificación y plasmado en un documento de

forma coherente.

f) Se ha defendido el resultado con argumentaciones y pruebas las verificaciones o refutaciones de las

hipótesis emitidas.

5. Reconoce las características básicas, anatómicas y fisiológicas, de los órganos y aparatos implicados en las funciones de relación y reproducción, así como algunas de sus alteraciones más frecuentes.

a) Se ha identificado la función de relación como un conjunto de procesos de obtención de información, procesado de la misma y elaboración de una respuesta.

b) Se han reconocido los órganos fundamentales del sistema nervioso, identificando los órganos de los sentidos y su función principal.

c) Se han identificado los factores sociales que repercuten negativamente en la salud como el estrés y el consumo de sustancias adictivas.

d) Se ha diferenciado entre reproducción y sexualidad.

e) Se han reconocido las principales diferencias del aparato reproductor masculino y femenino, identificando la función principal de cada uno.

f) Se han comparado los diferentes métodos anticonceptivos, valorando su eficacia e importancia en la prevención de las enfermedades de transmisión sexual.

g) Se ha valorado la sexualidad propia y de las personas que nos rodean, adquiriendo actitudes de respeto hacia las diferentes opciones.

6. Diferencia la salud de la enfermedad, relacionando los hábitos de vida con las enfermedades más frecuentes, reconociendo los principios básicos de defensa contra las mismas.

a) Se han identificado situaciones de salud y de enfermedad para las personas.

b) Se han descrito los mecanismos encargados de la defensa del organismo.

c) Se han identificado y clasificado las enfermedades infecciosas y no infecciosas más comunes en la población, y reconocido sus causas, la prevención y los tratamientos.

d) Se han relacionado los agentes que causan las enfermedades infecciosas habituales con el contagio producido.

e) Se ha entendido la acción de las vacunas, antibióticos y otras aportaciones de la ciencia médica para el tratamiento y prevención de enfermedades infecciosas.

f) Se ha reconocido el papel que tienen las campañas de vacunación en la prevención de enfermedades infecciosas.

g) Se ha descrito el tipo de donaciones que existen y los problemas que se producen en los trasplantes.

h) Se ha valorado la importancia del empleo de los equipos de protección individualizada en la realización de trabajos prácticos relacionados con el entorno profesional.

i) Se han buscado e interpretado informaciones estadísticas relacionadas con la salud y la enfermedad adoptando una actitud crítica ante las mismas.

7. Reconoce, plantea y analiza situaciones relacionadas con la energía en sus distintas formas y el consumo energético, valorando las consecuencias del uso de energías renovables y no renovables.

a) Se han identificado situaciones de la vida cotidiana en las que queda de manifiesto la intervención de la energía.

b) Se han reconocido diferentes fuentes de energía.

c) Se han analizado diferentes situaciones aplicando la Ley de conservación de la energía y el principio de degradación de la misma.

d) Se han descrito procesos relacionados con el mantenimiento del organismo y de la vida en los que se aprecia claramente el papel de la energía.

e) Se han relacionado la energía, el calor y la temperatura manejando sus unidades de medida.

f) Se han establecido grupos de fuentes de energía renovable y no renovable.

g) Se ha debatido de forma argumentada sobre las ventajas e inconvenientes (obtención, transporte y utilización) de las fuentes de energía renovable y no renovable, utilizando las TIC para obtener y presentar la información.

h) Se han identificado y manejado las magnitudes físicas básicas a tener en cuenta en el consumo de electricidad en la vida cotidiana.

i) Se han analizado los hábitos de consumo y ahorro eléctrico y establecido líneas de mejora en los mismos basándose en la realización de cálculos del gasto de energía en aparatos electrodomésticos y proponiendo soluciones de ahorro justificados con datos.

j) Se han clasificado las centrales eléctricas y descrito la transformación energética en las mismas debatiendo las ventajas y desventajas de cada una de ellas.

k) Se ha analizado el tratamiento y control de la energía eléctrica, desde su producción hasta su consumo valorando los costes.

8. Aplica técnicas físicas o químicas, utilizando el material necesario, para la realización de prácticas de laboratorio sencillas, midiendo las magnitudes implicadas.

a) Se ha verificado la disponibilidad del material básico utilizado en un laboratorio.

b) Se han identificado y medido magnitudes básicas, entre otras, masa, peso, volumen, densidad, temperatura.

c) Se ha realizado alguna práctica de laboratorio para identificar identificado algún tipo de biomoléculas presentes en algún material orgánico.

d) Se ha descrito la célula y tejidos animales y vegetales mediante su observación a través de instrumentos ópticos.

e) Se han elaborado informes de ensayos en los que se incluye el procedimiento seguido, los resultados obtenidos y las conclusiones finales.

9. Reconoce las reacciones químicas que se producen en los procesos biológicos y en la industria argumentando su importancia en la vida cotidiana y describiendo los cambios que se producen.

a) Se han identificado reacciones químicas principales de la vida cotidiana, la naturaleza y la industria.

b) Se han descrito las manifestaciones de reacciones químicas.

c) Se han descrito los componentes principales de una reacción química y la intervención de la energía en la misma.

d) Se han reconocido algunas reacciones químicas tipo, como combustión, oxidación, descomposición, neutralización, síntesis, aeróbica, anaeróbica.

e) Se han identificado los componentes y el proceso de reacciones químicas sencillas mediante ensayos de laboratorio.

f) Se han elaborado informes utilizando las TIC sobre las industrias más relevantes: alimentarias, cosmética, reciclaje, describiendo de forma sencilla los procesos que tienen lugar en las mismas.

10. Reconoce y analiza críticamente la influencia del desarrollo tecnológico sobre la sociedad y el entorno proponiendo y valorando acciones para la conservación del equilibrio medioambiental.

a) Se ha analizado las implicaciones positivas de un desarrollo sostenible.

b) Se han propuesto medidas elementales encaminadas a favorecer el desarrollo sostenible.

c) Se han diseñando estrategias básicas para posibilitar el mantenimiento del medioambiente.

d) Se ha trabajado en equipo en la identificación de los objetivos para la mejora del medioambiente.

e) Se han reconocido los fenómenos de la contaminación atmosférica y los principales agentes causantes de la misma.

f) Se ha investigado sobre el fenómeno de la lluvia ácida, sus consecuencias inmediatas y futuras y cómo sería posible evitarla.

g) Se ha descrito el efecto invernadero argumentando las causas que lo originan o contribuyen y las medidas para su minoración.

h) Se ha descrito la problemática que ocasiona la pérdida paulatina de la capa de ozono, las consecuencias para la salud de las personas, el equilibrio de la hidrosfera y las poblaciones.

11. Valora la importancia del agua como base de la vida en la Tierra analizando la repercusión de las diferentes actividades humanas sobre la misma.

a) Se ha reconocido y valorado el papel del agua en la existencia y supervivencia de la vida en el planeta.

b) Se han analizado los efectos que tienen para la vida en la Tierra la contaminación y el uso irresponsable de los acuíferos.

c) Se han identificado posibles contaminantes en muestras de agua de distinto origen planificado y realizando ensayos de laboratorio.

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

3. CALIFICACIÓN

Calificación final de cada unidad: Vendrá dada por la media ponderada de las pruebas específicas y el trabajo del alumno según las observaciones del profesor en clase. Las faltas de asistencia en los días de examen se tienen que justificar por escrito para poder hacer dicha prueba al siguiente día de clase. En los boletines de la primera y la segunda evaluación aparecerá la nota media truncada. La calificación final de junio del alumnado será la media de las notas exactas obtenidas en las tres evaluaciones, redondeada a las unidades.

Recuperación ESO: Los alumnos/as con evaluación negativa en algún trimestre tendrán una recuperación de los bloques no superados en Junio. Aquellos que no obtengan una media exacta de aprobado en Junio deberán presentarse a un examen global en Septiembre.

Recuperación de la materia pendiente del curso anterior para alumnos de 3ºeso: Los alumnos/as con la asignatura pendiente del curso anterior recuperarán si realizan las actividades de refuerzo y recuperación propuestas por la profesora. Estas actividades deberán entregarse en las fechas acordadas. En mayo, la profesora decidirá si el alumno/a tiene que hacer una prueba escrita, bien porque no ha realizado las actividades de forma satisfactoria, o bien porque no ha alcanzado el nivel mínimo en la asignatura del presente curso.