Simple and Compound Probability

Probability

How likely something is to happen.

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Tossing a Coin  When a coin is tossed, there are two possible outcomes: heads (H) or tails (T) We say that the probability of the coin landing H is ½. And the probability of the coin landing T is ½.

Throwing Dice  When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6. The probability of any one of them is 1/6.

Probability 

In general:

Probability of an event happening = Number of ways it can happen Total number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)
Total number of outcomes: 6 (there are 6 faces altogether)

So the probability = 1 6

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked?

Number of ways it can happen: 4 (there are 4 blues)
Total number of outcomes: 5 (there are 5 marbles in total)

So the probability = 4 5 = 0,8

Probability Line

We can show probability on a Probability Line: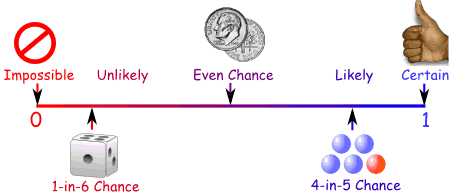

Probability is always between 0 and 1

Probability is Just a Guide

Probability does not tell us exactly what will happen, it is just a guide

Example: toss a coin 100 times, how many Heads will come up?

Probability says that heads have a ½ chance, so we can expect 50 Heads.
But when we actually try it we might get 48 heads, or 55 heads ... or anything really, but in most cases it will be a number near 50.

Learn more at Probability Index.

Words

Some words have special meaning in Probability:

Experiment or Trial: an action where the result is uncertain.

Tossing a coin, throwing dice, seeing what pizza people choose are all examples of experiments.

Sample Space: all the possible outcomes of an experiment

Example: choosing a card from a deck

There are 52 cards in a deck (not including Jokers)
So the Sample Space is all 52 possible cards: {Ace of Hearts, 2 of Hearts, etc... }

The Sample Space is made up of Sample Points:

Sample Point: just one of the possible outcomes

Example: Deck of Cards

• the 5 of Clubs is a sample point
• the King of Hearts is a sample point

"King" is not a sample point. As there are 4 Kings that is 4 different sample points.

Event: a single result of an experiment

Example Events:

• Getting a Tail when tossing a coin is an event
• Rolling a "5" is an event.

An event can include one or more possible outcomes:

• Choosing a "King" from a deck of cards (any of the 4 Kings) is an event
• Rolling an "even number" (2, 4 or 6) is also an event

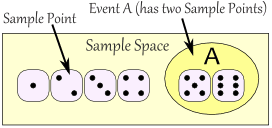The Sample Space is all possible outcomes. A Sample Point is just one possible outcome. And an Event can be one or more of the possible outcomes.

Hey, let's use those words, so you get used to them:

Example: Alex wants to see how many times a "double" comes up when throwing 2 dice.

Each time Alex throws the 2 dice is an Experiment.
It is an Experiment because the result is uncertain.

The Event Alex is looking for is a "double", where both dice have the same number. It is made up of these 6 Sample Points:

{1,1} {2,2} {3,3} {4,4} {5,5} and {6,6}

The Sample Space is all possible outcomes (36 Sample Points):

{1,1} {1,2} {1,3} {1,4} ... {6,3} {6,4} {6,5} {6,6}

These are Alex's Results:

Experiment	Is it a Double?
{3,4}	No
{5,1}	No
{2,2}	Yes
{6,3}	No
...	...

After 100 Experiments, Alex has 19 "double" Events ... is that close to what you would expect?

Activity: An Experiment with Dice

Let's throw two dice and add the scores ...

You will need: Two dice

Interesting point

Many people think that one of these cubes is called "a dice". But no!
The plural is dice, but the singular is die: i.e. 1 die, 2 dice.

The common die has six faces:

We usually call the faces 1, 2, 3, 4, 5 and 6.

Throwing Two Dice and Adding the Scores ...

Example: when one die shows 2 and the other shows 6 the total score is 2 + 6 = 8

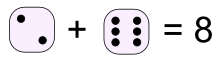
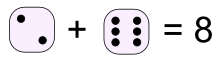
Question: Can you get a total of 8 any other way?

What about 6 + 2 = 8 (the other way around), is that a different way?
Yes! Because the two dice are different.

Example: imagine one die is colored red and the other is colored blue.
There are two possibilities:

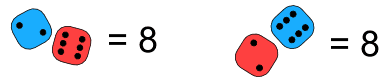So 2 + 6 and 6 + 2 are different.

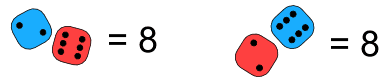
And you can get 8 with other numbers, such as 3 + 5 = 8 and 4 + 4 = 8

High, Low, and Most Likely

Before we start, let's think about what might happen.
Question: If you throw 2 dice together and add the two scores:

• 1. What is the least possible total score?
• 2. What is the greatest possible total score?
• 3. What do you think is the most likely total score?

The first two questions are quite easy to answer:

• 1. The least possible total score must be 1 + 1 = 2
• 2. The greatest possible total score must be 6 + 6 = 12
• 3. The most likely total score is ... ???

Are they all just as likely? Or will some happen more often?

To help answer the third question let us try an experiment.

The Experiment

Throw two dice together 108 times,
add the scores together each time,
record the scores in a tally table.

Why 108? That seems a strange number to choose. I will explain later.
You can record the results in this table using tally marks:

Added Scores	Tally	Frequency
2
3
4
5
6
7
8
9
10
11
12
	Total Frequency =	108

OK, Go!

...

...

Finished ...? Now draw a bar graph to show your results. Or you can use Data Graphs (Bar, Line and Pie) then print it out.
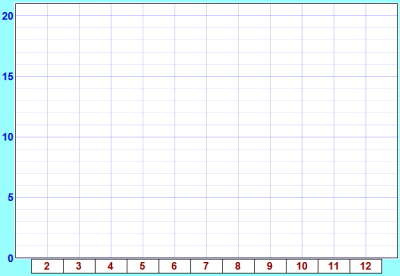You may get something like this:

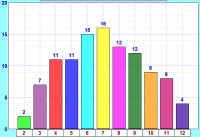• Are the bars all about the same height?
• If not ... why not?

So Why Did We Get That Shape?

The explanation is simple:

There is only one way to get a total of 2 (1 + 1),
but there are six ways of getting a total of 7 (1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2 and 6 + 1)

Here is a table of all possibile outcomes, and the totals. I have also shown what adds to 7 in bold.

		Score on One Die
		1	2	3	4	5	6
Score on the Other Die	1	2	3	4	5	6	7
	2	3	4	5	6	7	8
	3	4	5	6	7	8	9
	4	5	6	7	8	9	10
	5	6	7	8	9	10	11
	6	7	8	9	10	11	12

You can see there is only 1 way to get 2, there are 2 ways to get 3, and so on.

Let us count the ways of getting each total and put them in a table:

Total Score	Number of Ways to Get Score
2	1
3	2
4	3
5	4
6	5
7	6
8	5
9	4
10	3
11	2
12	1
	Total = 36

Can you see the Symmetry in this table?

• 2 and 12 have the same number of ways = 1 each
• 3 and 11 have the same number of ways = 2 each
• 4 and 10 have the same number of ways = 3 each
• 5 and 9 have the same number of ways = 4 each
• 6 and 8 have the same number of ways = 5 each

108 Throws

OK, why 108 throws? Well, only 36 throws might not give good results, 360 throws would be great, but take a long time, so 108 (which is 3 lots of 36) seems just right.
So let's multiply all these numbers by 3 to match our total of 108:

Total Score	Number of Ways to Get Score
2	3
3	6
4	9
5	12
6	15
7	18
8	15
9	12
10	9
11	6
12	3
	Total = 108

Those are the theoretical values, as opposed to the experimental ones you got from your experiment.
The theoretical values look like this in a bar graph:

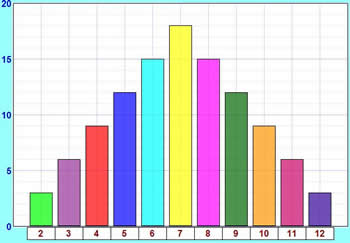
How do these theoretical results compare with your experimental results?

This graph and your graph should be quite similar, but they are not likely to be exactly the same, as your experiment relied on chance, and the number of times you did it was fairly small.
If you did the experiment a very large number of times, you should get results much closer to the theoretical ones.
And, by the way, we've now answered the question from near the beginning of the experiment:

What is the most likely total score?

• 7 has the highest bar, so 7 is the most likely total score.

Hey, is that why people talk about Lucky 7 ... ?

Probability

On the page Probability you will find a formula:

Probability of an event happening = Number of ways it can happen Total number of outcomes

Example: Probability of a total of 2

We know there are 36 possible outcomes.
And there is only 1 way to get a total score of 2.
So the probability of getting 2 is:

Probability of a 2 = 1 36

Doing that for each score gets us:

Total Score	Probability
2	1/36
3	2/36
4	3/36
5	4/36
6	5/36
7	6/36
8	5/36
9	4/36
10	3/36
11	2/36
12	1/36
	Total = 1

(Note: I didn't simplify the fractions)

The sum of all the probabilities is 1

PRACTICE