Christmas Reading - HLD

NASA Exercise: Survival on the Moon

ACTIVITY

Scenario: 

You are a member of a space crew originally scheduled to rendezvous with a 

mother ship on the lighted surface of the moon. However, due to mechanical 

difficulties, your ship was forced to land at a spot some 200 miles from the 

rendezvous point. During reentry and landing, much of the equipment aboard 

was damaged and, since survival depends on reaching the mother ship, the 

most critical items available must be chosen for the 200-mile trip. Below are 

listed the 15 items left intact and undamaged after landing. Your task is to 

rank order them in terms of their importance for your crew in allowing them 

to reach the rendezvous point. Place the number 1 by the most important item, 

the number 2 by the second most important, and so on through number 15 for 

the least important. 

Your Ranking NASA Ranking 
 _______ Box of matches _______ 
 _______ Food concentrate _______ 
 _______ 50 feet of nylon rope _______ 
 _______ Parachute silk _______ 
 _______ Portable heating unit _______ 
 _______ Two .45 caliber pistols _______ 
 _______ One case of dehydrated milk _______ 
 _______ Two 100 lb. tanks of oxygen _______ 
 _______ Stellar map _______ 
 _______ Self-inflating life raft _______ 
 _______ Magnetic compass _______ 
 _______ 20 liters of water _______ 
 _______ Signal flares _______ 
 _______ First aid kit, including injection needle _______ 
 _______ Solar-powered FM receiver-transmitter _______ 


Scoring: 
For each item, mark the number of points that your score differs from the 
NASA ranking, then add up all the points. Disregard plus or minus 
differences. The lower the total, the better your score. 

0 - 25 excellent 
26 - 32 good 
33 - 45 average 
46 - 55 fair 
56 - 70 poor -- suggests use of Earth-bound logic 
71 - 112 very poor – you’re one of the casualties of the space program! 
... published in the July 1999 issue of the NightTimes 

Movimiento Rectilineo Uniforme

Polynomials

A polynomial looks like this:

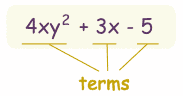example of a polynomial this one has 3 terms

Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term") ... so it says "many terms"

A polynomial can have:

constants (like 3, -20, or ½)

variables (like x and y)

exponents (like the 2 in y2), but only 0, 1, 2, 3, ... etc are allowed

that can be combined using addition, subtraction, multiplication and division ...

... except ...

... not division by a variable (so something like 2/x is right out)

So:

A polynomial can have constants, variables and exponents,
but never division by a variable.

Polynomial or Not?

These are polynomials:

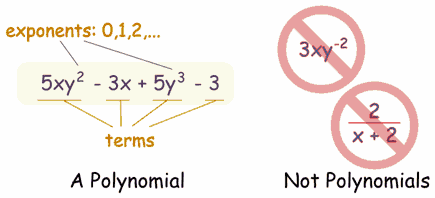
3x
x - 2
-6y² - (⁷/₉)x
3xyz + 3xy²z - 0,1xz - 200y + 0,5
512v⁵+ 99w⁵
5

(Yes, even "5" is a polynomial, one term is allowed, and it can even be just a constant!)
And these are not polynomials

• 3xy^-2 is not, because the exponent is "-2" (exponents can only be 0,1,2,...)
• 2/(x+2) is not, because dividing by a variable is not allowed
• 1/x is not either
• √x is not, because the exponent is "½"

But these are allowed:

• x/2 is allowed, because you can divide by a constant
• also 3x/8 for the same reason
• √2 is allowed, because it is a constant (= 1,4142...etc)

Monomial, Binomial, Trinomial

There are special names for polynomials with 1, 2 or 3 terms: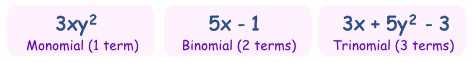

How do you remember the names? Think cycles!

There is also quadrinomial (4 terms) and quintinomial (5 terms),
but those names are not often used.

Can Have Lots and Lots of Terms

Polynomials can have as many terms as needed, but not an infinite number of terms.

Variables

Polynomials can have no variable at all

Example: 21 is a polynomial. It has just one term, which is a constant.

Or one variable

Example: x⁴-2x²+x has three terms, but only one variable (x)

Or two or more variables

Example: xy⁴-5x²z has two terms, and three variables (x, y and z)

What is Special About Polynomials?

Because of the strict definition, polynomials are easy to work with.
For example we know that:

• If you add polynomials you get a polynomial
• If you multiply polynomials you get a polynomial

So you can do lots of additions and multiplications, and still have a polynomial as the result.

You can also divide polynomials (but the result may not be a polynomial).

Degree

The degree of a polynomial with only one variable is the largest exponent of that variable.

Example:

The Degree is 3 (the largest exponent of x)

For more complicated cases, read Degree (of an Expression).

Standard Form

The Standard Form for writing a polynomial is to put the terms with the highest degree first.

Example: Put this in Standard Form: 3x² - 7 + 4x³ + x⁶

The highest degree is 6, so that goes first, then 3, 2 and then the constant last:

x⁶ + 4x³ + 3x² - 7

POLYNOMIALS OPERATIONS

https://courses.lumenlearning.com/waymakercollegealgebra/chapter/characteristics-of-polynomials/

https://jeopardylabs.com/play/polynomial-operations-8

LEYENDA DEL TABLERO DE AJEDREZ