Polynomials

A polynomial looks like this:

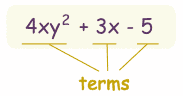example of a polynomial this one has 3 terms

Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term") ... so it says "many terms"

A polynomial can have:

constants (like 3, -20, or ½)

variables (like x and y)

exponents (like the 2 in y2), but only 0, 1, 2, 3, ... etc are allowed

that can be combined using addition, subtraction, multiplication and division ...

... except ...

... not division by a variable (so something like 2/x is right out)

So:

A polynomial can have constants, variables and exponents,
but never division by a variable.

Polynomial or Not?

These are polynomials:

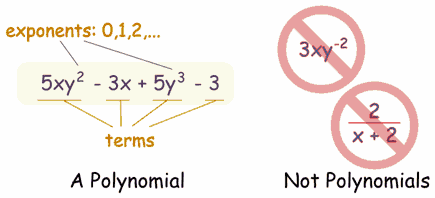
3x
x - 2
-6y² - (⁷/₉)x
3xyz + 3xy²z - 0,1xz - 200y + 0,5
512v⁵+ 99w⁵
5

(Yes, even "5" is a polynomial, one term is allowed, and it can even be just a constant!)
And these are not polynomials

• 3xy^-2 is not, because the exponent is "-2" (exponents can only be 0,1,2,...)
• 2/(x+2) is not, because dividing by a variable is not allowed
• 1/x is not either
• √x is not, because the exponent is "½"

But these are allowed:

• x/2 is allowed, because you can divide by a constant
• also 3x/8 for the same reason
• √2 is allowed, because it is a constant (= 1,4142...etc)

Monomial, Binomial, Trinomial

There are special names for polynomials with 1, 2 or 3 terms: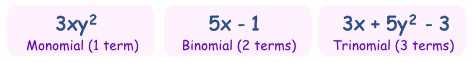

How do you remember the names? Think cycles!

There is also quadrinomial (4 terms) and quintinomial (5 terms),
but those names are not often used.

Can Have Lots and Lots of Terms

Polynomials can have as many terms as needed, but not an infinite number of terms.

Variables

Polynomials can have no variable at all

Example: 21 is a polynomial. It has just one term, which is a constant.

Or one variable

Example: x⁴-2x²+x has three terms, but only one variable (x)

Or two or more variables

Example: xy⁴-5x²z has two terms, and three variables (x, y and z)

What is Special About Polynomials?

Because of the strict definition, polynomials are easy to work with.
For example we know that:

• If you add polynomials you get a polynomial
• If you multiply polynomials you get a polynomial

So you can do lots of additions and multiplications, and still have a polynomial as the result.

You can also divide polynomials (but the result may not be a polynomial).

Degree

The degree of a polynomial with only one variable is the largest exponent of that variable.

Example:

The Degree is 3 (the largest exponent of x)

For more complicated cases, read Degree (of an Expression).

Standard Form

The Standard Form for writing a polynomial is to put the terms with the highest degree first.

Example: Put this in Standard Form: 3x² - 7 + 4x³ + x⁶

The highest degree is 6, so that goes first, then 3, 2 and then the constant last:

x⁶ + 4x³ + 3x² - 7

POLYNOMIALS OPERATIONS

https://courses.lumenlearning.com/waymakercollegealgebra/chapter/characteristics-of-polynomials/

https://jeopardylabs.com/play/polynomial-operations-8