Construcción de la caja
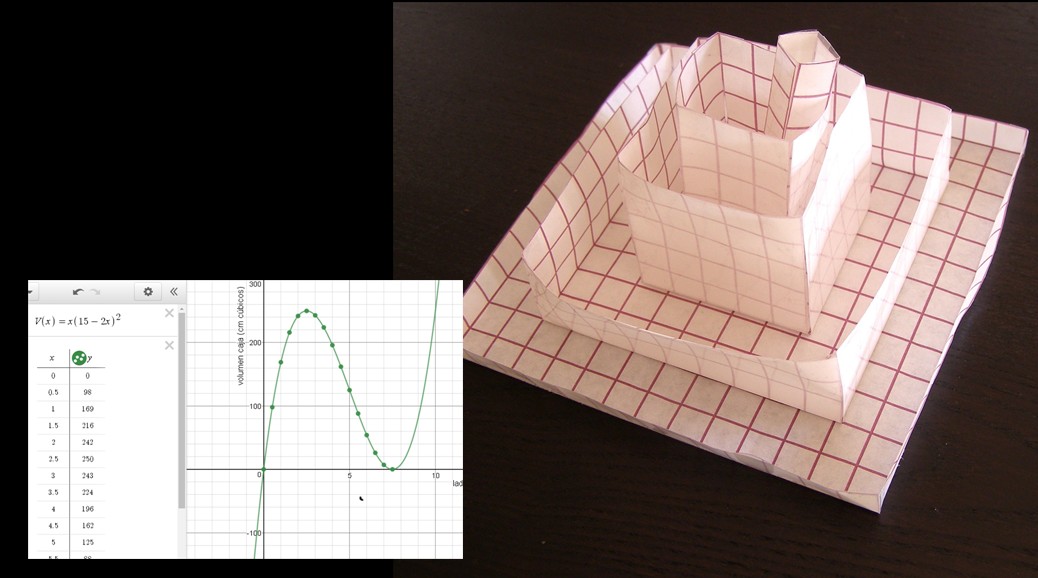
En la imagen puedes ver cómo se monta el tipo de caja sin tapa con el que vamos a trabajar.
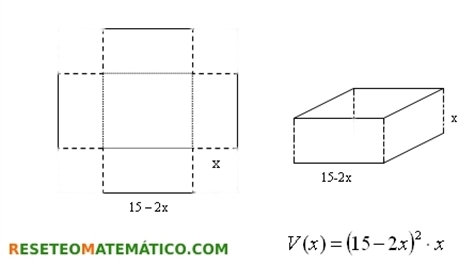
Empieza con un cuadrado de papel o cartulina de 15 cm de lado. Recorta cuatro cuadraditos iguales en las cuatro esquinas. Pliega dejando una base cuadrada. Une los lados de los rectángulos con celo para que estos hagan de paredes de la caja. Ya tienes una de tus cajas sin tapa.
Instrucciones:
Partimos de un cuadrado de 15 cm de lado.
¿Cómo cambia la capacidad de la caja abierta que formamos a partir de él, según el lado del cuadrado pequeño que recortamos en cada esquina va creciendo?
Hipótesis: alguien podría decir: “Según recorte cuadraditos más grandes, me quedará menos papel, con lo cual la capacidad de la caja será menor”.
¿Crees que cabría la misma cantidad de agua en la caja que resulta de cortar cuadraditos de 1cm de lado que en la que resulta de cortar cuadraditos de 7cm de lado?
¿Cuántos centímetros cúbicos caben en la caja que resulta de cortar cuadraditos de 1cm de lado?
¿Qué habéis hecho para averiguar cómo depende el volumen de la caja del lado del cuadradito que recortamos?
¿Qué habéis aprendido en relación al volumen de una caja?
ÁLGEBRA Y FUNCIONES
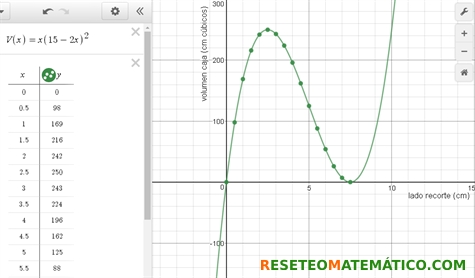
Identifican que en esta situación varía el lado del recorte y usan un símbolo (puede ser x u otro cualquiera) para referirse a cualquiera de sus valores. Identifica también que según varía el lado del recorte, x, varía también el volumen de la caja y usan un símbolo (por ejemplo V) para referirse a cualquiera de los valores del volumen. Escriben las operaciones que hay que hacer con x para obtener V. Es decir, la fórmula del volumen en función de x.
Representa gráficamente.
Anota en tu libreta tu hipóteis, tus conclusiones representándolas visualmente mediante dibujos, tablas, gráficas… Sube también las fotos de tus cajas y contesta las preguntas de la autoevaluación
Autoevaluación
- Tenemos una imagen mental de cómo es un centímetro de largo y cuánto ocupa un centímetro cúbico.
- Comprendemos que la capacidad o el volumen de una caja en centímetros cúbicos es el número de cubitos de centímetro cúbico que podemos meter dentro (idealmente).
- Entendemos la diferencia entre longitud y volumen y podemos explicarlo con nuestras propias palabras.
- Comprendemos que el volumen de una caja abierta depende de la medida del lado del cuadrado pequeño que cortamos en las esquinas.
- Sabemos que el volumen es nulo (cuando el recorte mide 0 cm), después aumenta hasta__________ (cuando el recorte es de ______ cm de lado) y disminuye hasta cero (cuando el recorte mide ______ cm de lado).
- Conocemos el máximo volumen que es __________. Se consigue cortando cuadraditos de __________cm de lado en cada esquina.


No comments:
Post a Comment