SIMULTANEOUS EQUATIONS - 3rd year
Simultaneous Equations
Simultaneous equations and linear equations, after studying this section, you will be able to:
- solve simultaneous linear equations by substitution
- solve simultaneous linear equations by substitution
- solve simultaneous linear equations by elimination
- solve simultaneous linear equations using straight line graphs
If an equation has two unknowns, such as 2y +
x = 20, it cannot have unique solutions. Two unknowns require two
equations which are solved at the sametime (simultaneously) − but even
then two equations involving two unknowns do not always give unique
solutions.
The video below works through examples of
simultaneous equations. The step-by-step example shows how to group like
terms and then add or subtract to remove one of the unknowns, to leave
one unknown to be solved.
This method is called solution by substitution.
It involves what it says − substitution − using
one of the equations to get an expression of the form ‘y = …’ or ‘x = …’
and substituting this into the other equation. This gives an equation
with just one unknown, which can be solved in the usual way. This value
is then substituted in one or other of the original equations, giving an
equation with one unknown.
Example
Solve the two simultaneous equations:
2y + x = 8 [1]
1 + y = 2x [2]
from [2] y = 2x -1 ← subtract 1 from each side
Substituting this value for y into [1] gives:
2(2x – 1) + x = 8
4x – 2 + x = 8 ← expand the brackets
5x – 2 = 8 ←tidy up
5x = 10 ←Add 2 to each side
x = 2 ←By dividing both sides by 5 the value of x is found.
Substitute the value of x into y = 2x – 1 gives
y = 4 - 1 = 3
So x = 2 and y = 3
NOTE:
- It is a good idea to label each equation. It helps you explain what you are doing − and may gain you method marks.
- This value of x can be substituted into equation [1] or [2], or into the expression for y: y = 2x − 1.
- Choose the one that is easiest!
- As a check, substitute the values back into each of the two starting equations.
The second method is called solution by elimination.
NOTE:The method is not quite as hard as it first seems, but it helps if you know why it works.
It works because of two properties of equations:- Multiplying (or dividing) the expression on each side by the same number does not alter the equation.
-
Adding two equations produces another valid equation:
e.g. 2x = x + 10 (x = 10) and x − 3 = 7 (x also = 10).
Adding the equations gives 2x + x − 3 = x + 10 + 7 (x also = 10).
The object is to manipulate the two equations
so that, when combined, either the x term or the y term is eliminated
(hence the name) − the resulting equation with just one unknown can then
be solved:
Here
we will manipulate one of the equations so that when it is combined
with the other equation either the x or y terms will drop out. In this
example the x term will drop out giving a solution for y. This is then
substituted into one of the otiginal equations.
Label your equations so you know which one your are working with at each stage.
Equation [1] is 2y + x = 8
Equation [2] is 1 + y = 2x
Rearrange one equation so it is similar to the other.
[2] y – 2x = -1
also 2 x [1] gives 4y + 2x = 16 which we call [3]
[2] y – 2x = -1
[3] 4y +2x = 16
[2] + [3] gives 5y = 15
so y = 3
substituting y = 3 into [1] gives 1 + (3) = 2x
so 2x = 4, giving x = 2 and y = 3
Solving simultaneous linear equations using straight line graphs
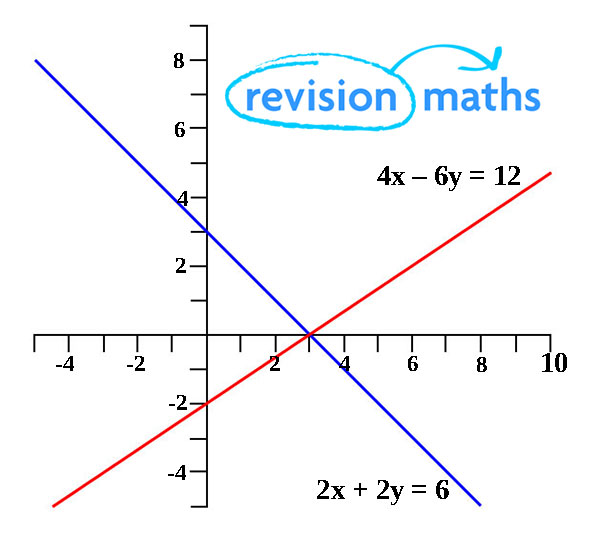
The 2 lines represent the equations '4x - 6y = -4' and '2x + 2y = 6'.
There is only one point the two equations cross.
Because the graphs of 4x - 6y = 12 and 2x + 2y = 6 are straight lines, they are called linear equations.
TRABAJAMOS LA AUTOESTIMA I
LA PEQUEÑA LUCIÉRNAGA
Había una vez una comunidad de luciérnagas que habitaba el interior de un gigantesco lampati,
uno de los árboles más majestuosos y antiguos de Tailandia. Cada noche,
cuando todo se volvía oscuro y apenas se escuchaba el leve murmurar de
un cercano río, todas las luciérnagas salían del árbol para mostrar al
mundo sus maravillosos destellos. Jugaban a hacer figuras con sus luces,
bailando al son de una música inventada para crear un sinfín de
centelleos luminosos más resplandeciente que cualquier espectáculo de
fuegos artificiales.
Pero entre todas las luciérnagas del lampati había una muy pequeñita a la que no le gustaba salir a volar.
– No, hoy tampoco quiero salir a volar -decía todos los días la
pequeña luciérnaga-. Id vosotros que yo estoy muy bien aquí en casita.
Tanto sus padres como sus abuelos, hermanos y amigos esperaban con
ilusión la llegada del anochecer para salir de casa y brillar en la
oscuridad. Se divertían tanto que no comprendían por qué la pequeña
luciérnaga no les quería acompañar. Le insistían una y otra vez, pero no
había manera de convencerla. La pequeña luciérnaga siempre se negaba.
-¡Que no quiero salir afuera! -repetía una y otra vez-. ¡Mira que sois pesados!
Toda la colonia de luciérnagas estaba muy preocupada por su pequeña compañera.
-Tenemos que hacer algo -se quejaba su madre-. No puede ser que siempre se quede sola en casa sin salir con nosotros.
Toda la colonia de luciérnagas estaba muy preocupada por su pequeña compañera.
-Tenemos que hacer algo -se quejaba su madre-. No puede ser que siempre se quede sola en casa sin salir con nosotros.
-No te preocupes, mujer -la consolaba el padre-. Ya verás como cualquier día de estos sale a volar con nosotros.
Pero los días pasaban y pasaban y la pequeña luciérnaga seguía encerrada en su cuarto.
Una noche, cuando todas las luciérnagas habían salido a volar, la
abuela de la pequeña se le acercó y le preguntó con mucha delicadeza:
-¿Qué es lo que ocurre, mi pequeña? ¿Por qué no quieres venir nunca con nosotros a brillar en la oscuridad?
-¿Qué es lo que ocurre, mi pequeña? ¿Por qué no quieres venir nunca con nosotros a brillar en la oscuridad?
-Es que no me gusta volar-, respondió la pequeña luciérnaga.
-Pero, ¿por qué no te gusta volar ni mostrar tu maravillosa luz? -insistió la abuela luciérnaga.
-Pero, ¿por qué no te gusta volar ni mostrar tu maravillosa luz? -insistió la abuela luciérnaga.
-Pues… -explicó al fin la pequeña luciérnaga-. Es que para qué voy a
salir si nunca podré brillar tanto como la luna. La luna es grande, y
muy brillante, y yo a su lado no soy nada. Soy tan diminuta que en
comparación parezco una simple chispita. Por eso siempre me quedo en
casa, porque nunca podré brillar tanto como la luna.
La abuela había escuchado con atención las razones de su nieta, y le contestó:
-¡Ay, mi niña! hay una cosa de la luna que debería saber y, visto lo visto, desconoces. Si al menos salieras de vez en cuando, lo habrías descubierto, pero como siempre te quedas en el árbol, pues no lo sabes.
-¡Ay, mi niña! hay una cosa de la luna que debería saber y, visto lo visto, desconoces. Si al menos salieras de vez en cuando, lo habrías descubierto, pero como siempre te quedas en el árbol, pues no lo sabes.
-¿Qué es lo que he de saber y no sé? -preguntó con impaciencia la pequeña luciérnaga.
-Tienes que saber que la luna no tiene la misma luz todas las noches -le contestó la abuela-. La luna es tan variable que cada día es diferente. Hay días en los que es grande y majestuosa como una pelota, y brilla sin cesar en el cielo. Pero hay otros días en los que se esconde, su brillo desaparece y el mundo se queda completamente a oscuras.
-Tienes que saber que la luna no tiene la misma luz todas las noches -le contestó la abuela-. La luna es tan variable que cada día es diferente. Hay días en los que es grande y majestuosa como una pelota, y brilla sin cesar en el cielo. Pero hay otros días en los que se esconde, su brillo desaparece y el mundo se queda completamente a oscuras.
-¿De veras hay noches en las que la luna no sale? -preguntó sorprendida la pequeña luciérnaga.
-Así es -le confirmó la abuela. La luna es muy cambiante. A veces
crece y a veces se hace pequeñita. Hay noches en las que es grande y
roja y otras en las que desaparece detrás de las nubes. En cambio tú, mi
niña, siempre brillarás con la misma fuerza y siempre lo harás con tu
propia luz.
La pequeña luciérnaga estaba asombrada ante tal descubrimiento. Nunca
se había imaginado que la luna pudiese cambiar y que brillase o se
escondiese según los días.
Y a partir de aquel día, la pequeña luciérnaga decidió salir a volar y
a bailar con su familia y sus amigos. Así fue como nuestra pequeña
amiguita aprendió que cada uno tiene sus cualidades y por tanto, cada
uno debe brillar con su propia luz.
DECIMAL NUMBERS
Naming decimal places
A decimal number is made of an integer part, placed on the left side of a decimal point, and a fractional part, placed on the right side of a decimal point. As a matter a fact, decimals are numbers which tells us how many parts of a whole we have. We use them to mark measure units of things that are not completely whole.
All the place values of the numbers depend on position on the left or right side of a decimal point. Look at the example with more digits.
Let’s take a look at, for example the number 1,987,654,321.123456,
The first digit before the decimal point represents the ones (number 1),
-the second stands for the tens (number 2), the third for the hundreds (number 3),
-the fourth for the thousands (number 4, after the comma),
-the fifth for the ten thousands (number 5),
-the sixth for the hundred thousands (number 6),
-the seventh for the millions (number 7, after the second comma),
-the eight for the ten millions (number 8),
-the ninth for the hundred millions (number 9) and
-the tenth for the billions (number 1, after the third comma).
All digits after the decimal point are called decimals.
-The first digit represents tenths (number 1),
-the second digit stands for the hundredths (number 2),
-third for the thousandths (number 3),
-fourth for the ten thousandths (number 4),
-fifth for the hundred thousandths (number 5),
-sixth for the millionths (number 6)
Let’s take a look at, for example the number 1,987,654,321.123456,
The first digit before the decimal point represents the ones (number 1),
-the second stands for the tens (number 2), the third for the hundreds (number 3),
-the fourth for the thousands (number 4, after the comma),
-the fifth for the ten thousands (number 5),
-the sixth for the hundred thousands (number 6),
-the seventh for the millions (number 7, after the second comma),
-the eight for the ten millions (number 8),
-the ninth for the hundred millions (number 9) and
-the tenth for the billions (number 1, after the third comma).
All digits after the decimal point are called decimals.
-The first digit represents tenths (number 1),
-the second digit stands for the hundredths (number 2),
-third for the thousandths (number 3),
-fourth for the ten thousandths (number 4),
-fifth for the hundred thousandths (number 5),
-sixth for the millionths (number 6)
There are larger and smaller place values, but these ones are used the most. It doesn’t matter how large the number of digits is, they can be read and understood with ease. Test the knowledge with worksheets.
Sequences
The general term of a sequence is the expression that represents all the terms of the sequence (there are usually infinitive terms!).The general term is expressed by an algebraic expression that shows therelation between the that term.
A
sequenceis
increasing
if
every
term
is
greater
the
previous
one
and
a
sequence
is decreasing
if
every
term
is
less
than
the
previous.
Some
sequences
are
special
because
they
have
a
singular
structure.
The
difference of
any
two
successive
terms
of
the
sequence
is aconstant. They
can
be
defined
by
the
first
term
and
the
constant
value
called
common difference. These
sequences
always increase
(or
decrease). These
sequences
are
called
arithmetic
progressions.
A geometric progression is a sequence where every term is generated by multiplying the previous one by a fixed number called the common ratio of the progression.
TEST DE INTELIGENCIA EMOCIONAL PARA LOS NIÑOS
En cada frase debe evaluar y cuantificar su capacidad en el uso de la habilidad descrita. Antes de responder, intenta pensar en situaciones reales en las que hayas tenido que utilizar dicha habilidad y no pretendas responder de acuerdo a lo que usted crea que sería lo correcto.
CAPACIDAD EN GRADO
BAJO
|
CAPACIDAD EN GRADO
ALTO
|
||||
1
|
2
|
3
|
4
|
5
|
6
|
No.
|
HABILIDADES
|
PUNTOS
|
| 1 | Identificar cambios del estímulo fisiológico | |
| 2 | Relajarse en situaciones de presión | |
| 3 | Actuar de modo productivo mientras está enojado | |
| 4 | Actuar de modo productivo mientras está ansioso | |
| 5 | Tranquilizarse rápidamente mientras está enojado | |
| 6 | Asociar diferentes indicios físicos con emociones diversas | |
| 7 | Usar el diálogo interior para controlar estados emocionales | |
| 8 | Comunicar los sentimientos de un modo eficaz | |
| 9 | Pensar con sentimientos negativos sin angustiarse | |
| 10 | Mantenerse en calma cuando es blanco del enojo de otros | |
| 11 | Saber cuando tiene pensamientos negativos | |
| 12 | Saber cuando su "discurso interior" es positivo | |
| 13 | Saber cuando empieza a enojarse | |
| 14 | Saber como interpreta los acontecimientos | |
| 15 | Conocer qué sentimientos utiliza actualmente | |
| 16 | Comunicar con precisión lo que experimenta | |
| 17 | Identificar la información que influye sobre sus interpretaciones | |
| 18 | Identificar sus cambios de humor | |
| 19 | Saber cuándo está a la defensiva | |
| 20 | Calcular el impacto que su comportamiento tiene en los demás | |
| 21 | Saber cuando no se comunica con sentido | |
| 22 | Ponerse en marcha cuando lo desea | |
| 23 | Recuperarse rápidamente después de un contratiempo | |
| 24 | Completar tareas a largo plazo dentro del tiempo previsto | |
| 25 | Producir energía positiva cuando realiza un trabajo poco interesante | |
| 26 | Abandonar o cambiar hábitos inútiles | |
| 27 | Desarrollar conductas nuevas y más productivas | |
| 28 | Cumplir lo que promete | |
| 29 | Resolver conflictos | |
| 30 | Desarrollar el consenso con los demás | |
| 31 | Mediar en los conflictos con los demás | |
| 32 | Utilizar técnicas de comunicación interpersonal eficaces | |
| 33 | Expresar los pensamientos de un grupo | |
| 34 | Influir sobre los demás en forma directa o indirecta | |
| 35 | Fomentar la confianza con los demás | |
| 36 | Montar grupos de apoyo | |
| 37 | Hacer que los demás se sientan bien | |
| 38 | Proporcionar apoyo y consejo a los demás cuando es necesario | |
| 39 | Reflejar con precisión los sentimientos de las personas | |
| 40 | Reconocer la angustia de los demás | |
| 41 | Ayudar a los demás a controlar sus emociones | |
| 42 | Mostrar comprensión hacia los demás | |
| 43 | Entablar conversaciones íntimas con los demás | |
| 44 | Ayudar a un grupo a controlar sus emociones | |
| 45 | Detectar incongruencias entre las emociones o sentimientos de los demás y sus conductas |
POLYNOMIALS IDENTITIES
Algebraic Identities
(a + b)(a - b) = a2 - b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
Example 1: Simplify (3u + 5w)(3u – 5w)
Using the algebraic identities (a + b)(a - b) = a2 - b2, we substitute a for 3u and b for 5w.
(3u + 5w)(3u – 5w)
= (3u)2 – (5w)2
= 9u2 – 25w2
Thus (3u + 5w)(3u – 5w) = 9u2 – 25w2
Example 2 : Using the algebraic identities to simplify (3a + 7b)2
Using (a+b)2 = a2+2ab+b2
In this case we need to substitute 3a for a as well as 7b for b
(3a + 7b)2
= (3a)2 + 2(3a)(7b) + (7b)2
= 9a2+ 42ab + 49b2
Thus (3a + 7b)2 = 9a2+ 42ab + 49b2
Example 3: Simplify (5a – 7b)2
Using (a-b)2 = a2-2ab+b2 we have:
(5a – 7b)2
= (5a)2 – 2(5a) (7b) + (7b)2
= 25a2 – 70ab + 49b2.
Thus (5a – 7b)2 = 25a2 – 70ab + 49b2
PANEL DE LAS EMOCIONES
Si tenemos que definir las emociones nosotros pensamos que son
los sentimientos que tenemos desde dentro y que nos hacen estar de una
forma o de otra. En el diccionario nos dice que:
La emoción es un sentimiento breve e intenso producido por algo bueno o malo que nos impresiona mucho, una noticia inesperada, un regalo o una película nos puede causar mucha emoción, también las personas y las cosas nos producen emociones.
Vamos a trabajar la alegría, la tristeza, el enfado, el miedo y la satisfacción. Veremos que las emociones se relacionan unas con otras. Unas nos gustan más, otras menos, pero todas son importantes conocerlas, aceptarlas y controlarlas.
- Vemos una imagen.
- Pensamos de que emoción puede ser.
- Luego hablamos de nuestros sentimientos.
- Descubrimos palabras que están relacionadas con la imagen y con esa emoción.
- Hablamos de momentos en los que notamos ese sentimiento y qué podemos hacer con esa emoción.
- Hacemos el cartel de la emoción que hemos trabajado y lo pegamos en nuestro panel.
DÍA MUNDIAL DE LA BIBLIOTECA
Por iniciativa de la
Asociación Española de Amigos del Libro Infantil y Juvenil, desde 1997, en
colaboración con el Ministerio de Educación, Cultura y Deporte, cada 24
de octubre se celebra el Día de la Biblioteca, con el objetivo de
concienciar a la sociedad de la importancia de la lectura y como homenaje y
reconocimiento a la labor de los bibliotecarios/as.
Cada año se encarga a
un escritor y a un ilustrador, ambos de reconocido prestigio, la redacción del
pregón y el diseño del cartel que se difunde entre todas las bibliotecas de
España, asociados e interesados. Este año los seleccionados son el escritor Diego
Arboleda, Premio Nacional de Literatura Infantil 2014, y la
ilustradora Leticia Ruiz Fernández.
Con este motivo desde
la Junta de Andalucía se ha propuesto la semana del 26 al 30 de Octubre, para
dar más visibilidad a las bibliotecas de los centros. Nosotros desde el plan de
bibliotecas hemos decidido organizar un concurso de carteles y otro de lemas,
que se realizaran preferentemente en las horas de tutoría.
X CONCURSO “ LEMAS DE
LA BIBLIOTECA” BIBLIOTECA JORDI SIERRA I FABRA
Torre del
Mar a 7 de Octubre de 2015, con motivo de la celebración durante la semana del
26 al 30 de Octubre de la semana de la biblioteca se convoca el X concurso, en
este caso será de lemas: “lemas de la biblioteca”, con él intentaremos hacerla
más visible en nuestro centro y que los alumnos reflexionen sobre la
importancia de la lectura.
1.-
se desecharán todos aquellos
lemas que hagan referencia a violencia de cualquier tipo, tengan contenido
sexual u ofensivo y/o denigren la imagen
de la persona.
2.- Participantes: cualquier
persona miembro de la comunidad educativa que lo desee puede participar.
3.- Se podrán presentar en Word, A4 vertical, se admiten 2 lemas por
participante.
4.- Forma de presentación: Correo
electrónico, en archivo adjunto o en papel, respetando el mismo formato. Se
deberá enviar un mensaje de correo electrónico con el siguiente asunto:
X concurso de la biblioteca Jordi Sierra i Fabra a la
dirección
En el mensaje se adjuntará un
solo archivo en formato Word (.doc) donde aparecerán el título del relato, el nombre del
autor y su fecha de nacimiento así como el curso y clase a que pertenece el participante.
5.- Los trabajos se enviarán
antes del 30
de octubre.
6. Habrá premios para los
ganadores de cada categoría.
7.- El jurado estará compuesto
por miembros del proyecto de biblioteca.
8.- El fallo del jurado será
inapelable.
XI CONCURSO “ CARTELES
DE LA BIBLIOTECA” BIBLIOTECA JORDI SIERRA I FABRA
Torre del
Mar a 7 de Octubre de 2015, con motivo de la celebración durante la semana del
26 al 30 de Octubre de la semana de la biblioteca se convoca el X concurso, en
este caso será de lemas: “Carteles de la biblioteca”, con él intentaremos
hacerla más visible en nuestro centro y que los alumnos reflexionen sobre la
importancia de la lectura.
1.-
se desecharán todos aquellos
lemas que hagan referencia a violencia de cualquier tipo, tengan contenido
sexual u ofensivo y/o denigren la imagen
de la persona.
2.- Participantes: cualquier
persona miembro de la comunidad educativa que lo desee puede participar.
3.- Se podrán presentar en cartulinas o media cartulina, se admitirán 2 por participante.
4.- Forma de presentación, se
entregarán en mano al profesor de lengua y por detrás aparecerá:
XI concurso de la biblioteca Jordi Sierra i Fabra.
Nombre y apellidos :
Curso:
5.- Los trabajos se entregarán
antes del 30
de octubre.
6. Habrá premios para los
ganadores de cada categoría.
7.- El jurado estará compuesto
por miembros del proyecto de biblioteca.
8.- El fallo del jurado será
inapelable.
Subscribe to:
Comments (Atom)






























