Funciones Lineales
Objetivos de Aprendizaje
· Definir las funciones lineales y describir sus características.
· Comparar funciones lineales proporcionales y no proporcionales (afín).
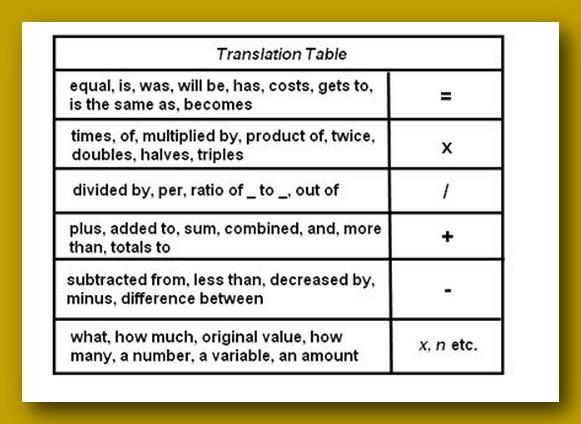
· Explicar los componentes de la ecuación de una función lineal.
Cada mañana Miguel se prepara una taza de café poniendo 2.5 cucharadas de granos de café molidos en su cafetera. A veces, cuando se ha desvelado la noche anterior, necesita 2 tazas de café para despertar, por lo que pone doble cantidad en la cafetera. Si tiene invitados a cenar y quiere servir café con el postre, prepara una cantidad mayor de café. Su receta es simple — pone 2.5 cucharadas por cada taza que quiere preparar.
Miguel puede fácilmente adaptar su receta, porque hay una relación entre la cantidad de granos de café y el número de tazas — al aumentar la cantidad de café, aumenta también la cantidad de granos necesarios. Veamos cómo se ve ésta relación en una gráfica.
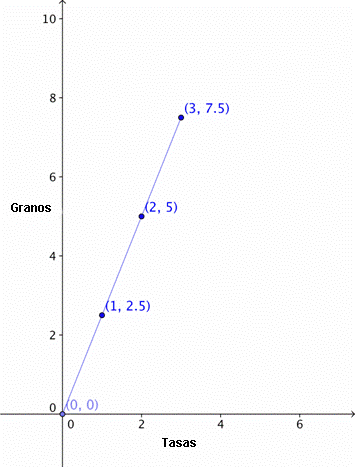
Podemos ver que ésta relación es una función— para cada valor independiente (tazas de café), hay un único valor dependiente (cucharadas de granos necesarias). También podemos ver que la gráfica de pares deentradas y salidas es una línea recta. Esto la hace una función lineal — una función es lineal si su gráfica forma una línea recta. La línea es recta porque las variables cambian con una tasa constante. Ésa es otra característica de las funciones lineales — tienen una tasa de cambio constante.
Veamos otro tipo de funciones lineales para entender mejor cómo funcionan.
Mientras que Miguel se toma su café, decide comparar algunos planes de servicios móviles para ver cuál le parece mejor. Su compañía celular le ofrece dos planes. El plan básico cobra 7 centavos por mensaje de texto mandado o recibido. El plan avanzado le permite a Miguel mandar textos, fotos y video, y sólo cobra 2 centimos por mensaje. ¡Perfecto! Pero espera — el plan avanzado tienen un cargo mensual fijo de 10€. Entonces ¿Cómo va a decidir Miguel cuál plan le conviene más?
¡Lo sé! Ambos planes son funciones — el costoe de mandar textos depende del número de textos enviados. Si representamos cada uno, podemos comparar cómo varían los costes.
Empecemos con el plan básico. Podemos calcular el coste (y) de mandar y recibir cualquier número de mensajes (x) con la ecuación simple y = 0.07x. (Usando 0.07 en lugar de 7, el coste (y) será medido en euros en lugar de centimos.) Con ésta ecuación podemos calcular los siguientes puntos:
# de Textos
|
Coste
|
0
|
0.00
|
10
|
0.70
|
100
|
7.00
|
200
|
14.00
|
La gráfica de esos puntos se ve así — una línea recta desde (0,0).
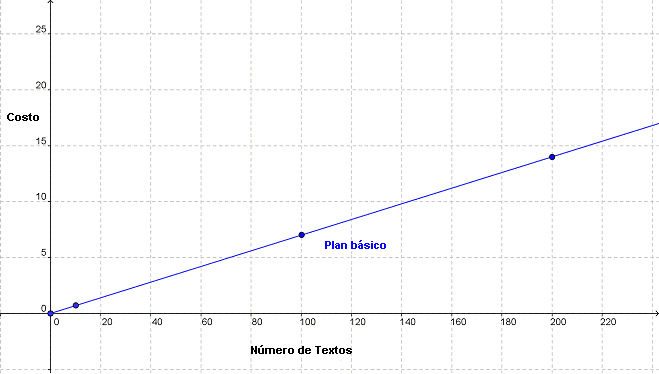
Ahora veremos el plan avanzado. Para calcular el coste (y) de mandar y recibir x número de mensajes por mes con éste plan, podemos empezar con una ecuación muy parecida a la que usamos antes: y = 0.02x, porque cada mensaje cuesta 2 centimos. Pero ¿recuerdas el cargo mensual? Tenemos que sumar 10€, y nuestra ecuaciónse vuelve y = 0.02x + 10. Con ésta ecuación, podemos calcular los siguientes valores para el plan avanzado:
# de Textos
|
Costo
|
0
|
10.00
|
10
|
10.20
|
100
|
12.00
|
200
|
14.00
|
Representando esos puntos.
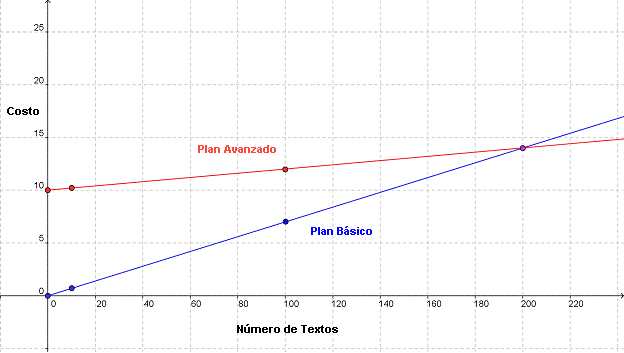
Ahora la diferencia entre los dos planes es clara — si Miguel manda menos de 200 textos al mes, el plan básico es más barato. Si manda más de 200 textos, habrá ahorrado dinero usando el plan avanzado. Saber esto es útil para Miguel, pero nosotros estamos más interesados en las funciones. Ambas son líneas rectas con una tasa de cambio estable, por lo que son funciones lineales. Pero el plan básico incluye el origen, mientras que el plan avanzado no.
Hay algo especial con las funciones lineales que incluyen el origen — hay una relación multiplicativa simple entre las variables independientes y las variables dependientes. Esto significa que las variables tienen una relación proporcional, y éstas son funciones proporcionales. Para las funciones proporcionales, si multiplicamos ambas variables por el mismo número, su relación se mantendrá. Por ejemplo, volviendo a la tabla del plan básico:
# de Textos
|
Costo
|
0
|
0.00
|
1
|
0.07
|
10
|
0.70
|
100
|
7.00
|
200
|
14.00
|
El coste de un texto = 0.07. Si Miguel quiere encontrar el coste de mandar 10 textos bajo este plan, él podría tomar la ecuación 1 = 0.07 y multiplicar ambos lados por 10. Encontraría un coste de 0.70 por 10 textos. Si multiplicamos ambas cantidades por 0 veríamos que la gráfica debe pasar por el origen. Esto tiene sentido, porque 0 mensajes cuestan 0€.
Ahora veamos la otra función, para el plan avanzado:
# de Textos
|
Costo
|
0
|
10.00
|
1
|
10.02
|
10
|
10.20
|
100
|
12.00
|
200
|
14.00
|
El costo de un texto = 10.02€. ¿Podemos calcular el coste de 10 textos multiplicando ambos lados de la relación por 10? No — ¡10 textos no cuestan 100.20€! ¿Qué salió mal? A pesar de que el plan avanzado es una función lineal, no es una función proporcional — las variables dependiente e independiente no están relacionadas por sólo una constante y no tienen una relación proporcional. Con relaciones no proporcionales, multiplicar la entrada y la salida por el mismo número no funciona. Por esto, funciones lineales no proporcionales no incluyen el origen — el multiplicar la entrada por 0 no hará la salida 0